Search algorithms: Part 1

Searching is present in our daily life, from finding a contact in an alphabetically sorted contact list or even searching a word in the dictionary.

We have countless scenarios where we need to find something, so having the right approach to do so can make our lives easier!

There are many search algorithms, but I will explain the two most common ones: linear search and binary search.

Linear Search

Linear search is the simplest one. You just iterate over your list until you find the target element. When you reach it, return the index at which it was found. Otherwise, if such element is not present, return -1.

Below we can find a simple implementation of this approach.

public static int search(int[] array, int target) {
        for(int i=0;i!=array.length;i++) {
            if(array[i]==target) return i;
        }
        return -1;
    }

About the time complexity, in the worst case we need to iterate over the entire array (target element in the last position or the element does not exist). Due to this, our time complexity is O(n).

As we can easily see, the space complexity of O(1).

Binary Search

Binary search is faster than linear search but only works on sorted lists. This means that if your input array is not sorted, you need to sort it first. This will have an impact on the time and space complexity analysis.

Binary search works first by finding the middle point of our array and comparing the value at this index with our target value. If the middle element is indeed the element that we are looking for, we return the middle point index. What happens if our target is not there?

Now comes the magic of having the array sorted.

We know that every element on the left side of the middle element is smaller than the middle element and that every element on the right side of the middle element is bigger than it. We just need to verify if our target element is bigger or smaller than this middle element. In the next step, we either analyze the left side of the array or the right side, meaning that in each step of analysis we cut in half the number of elements that we need to visit (this is the famous technique of divide and conquer). We do this until we find the element or no element is found.

We can implement binary search using recursion or using an iterative approach. Below you can find the recursive implementation.

//assuming that the input array is sorted
public static int binarySearchRecursive(int[] array, int target, int low, int high) {
        if(high<low) return -1;
        int middle = (low+high)/2;
        if(array[middle]==target) return middle;
        if(target>array[middle]) low = middle+1;
        else high=middle-1;
        return binarySearchRecursive(array,target,low, high);
    }

The following figures show the simple reasoning in finding a specific element in an array, using binary search.

Let's say that this is our original array and that our purpose is to find number 3.

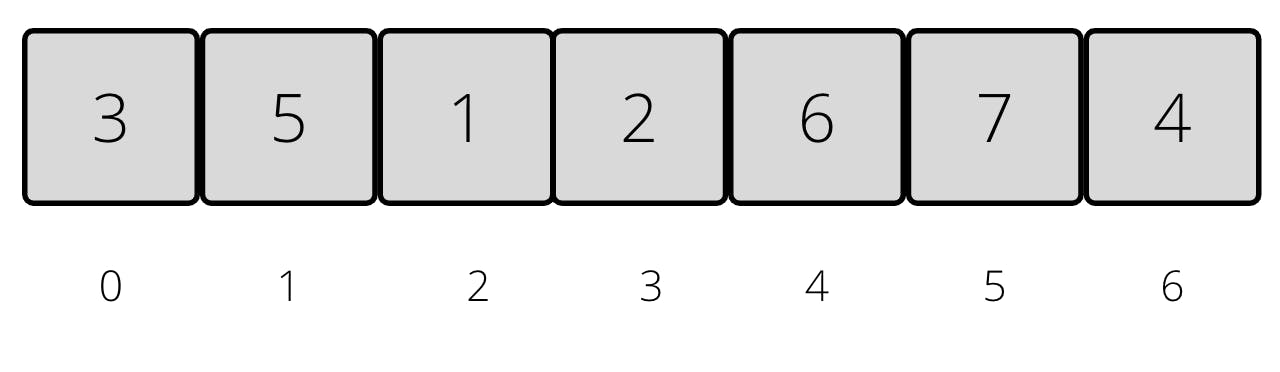
Our first step, as mentioned before, is sorting our array.

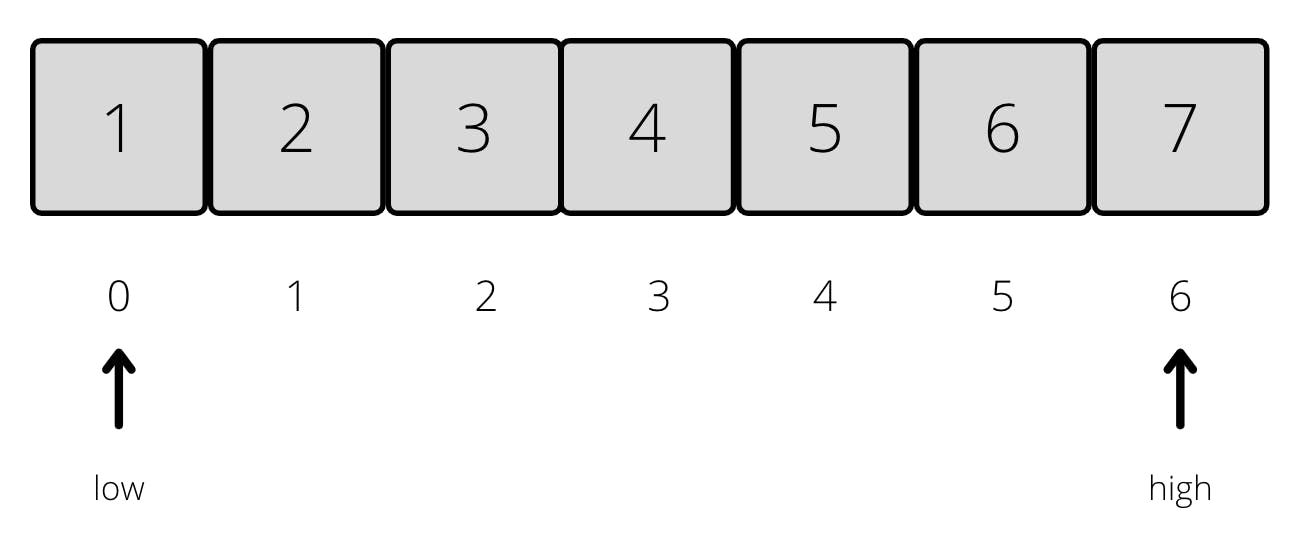
Now we need to find our middle element. Its index is 3 (6+0) and the value is 4. Let's compare 3 and 4. Since 3 is smaller than 4, we now focus our attention on the left side of the array (represented with the blue border).

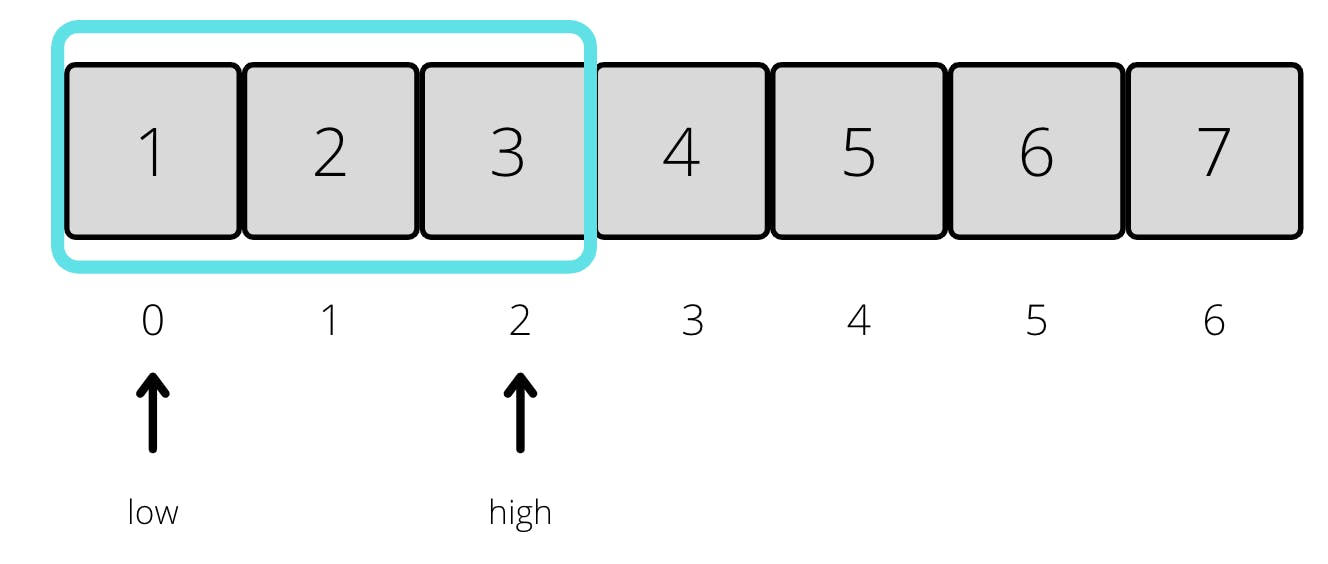
Now we do the same. Compute the middle element, which is 2, compare it with our target value 3. 3 is bigger than 2, so this means that we will only in the right side of 2.

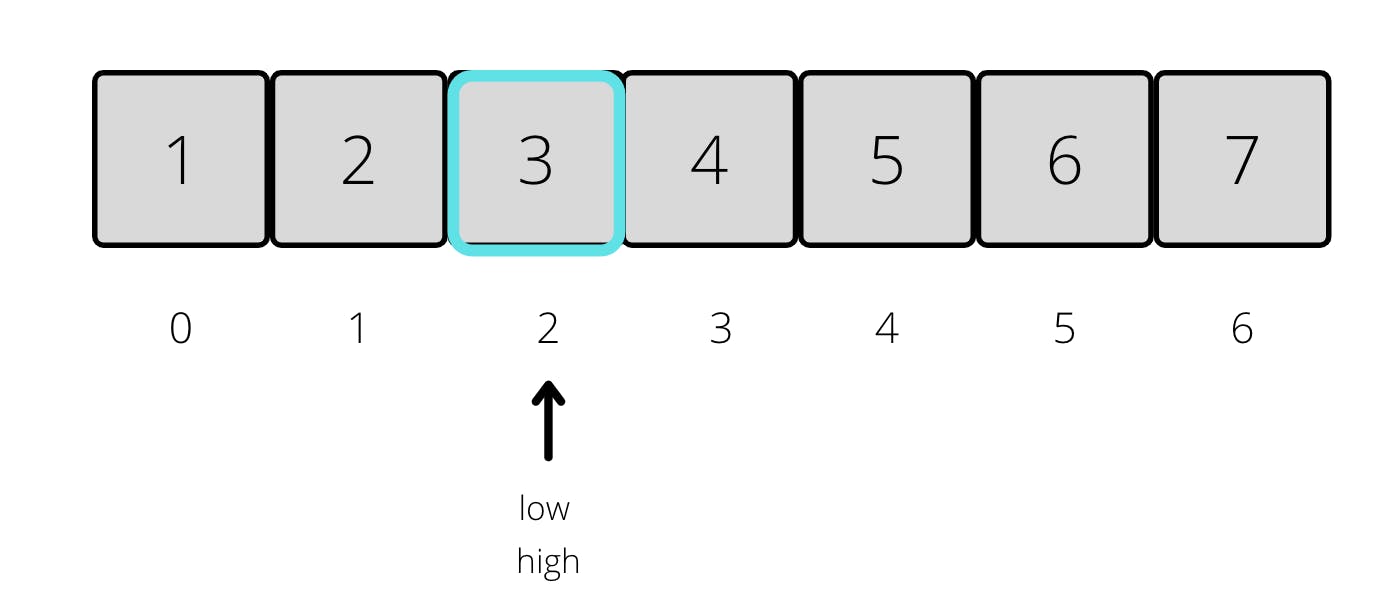
Now our middle element is equal to 3, which happens to be the element to the element we were looking for! Our algorithm would return 2, which is the index at which 3 is located.

Time and Space complexity

We need to be careful when analyzing the time and space complexity of this algorithm. We might be tempted to say that our time complexity is O(log(n)) and space complexity of O(log(n)) [due to the stack calls we do in our recursion]. That would be true if our array was sorted already. But that is not the worst-case scenario. In the worst-case scenario, we need to force the sorting of our input array.

Thus, we must take into consideration the "cost" of sorting the array in our final computations of the time and space complexities. Now, this "cost" of sorting will depend only on the sorting algorithm that you choose. Different algorithms have different time and space complexities, meaning different "costs". I will base my sorting on merge sort, which has an average time complexity of O(n * log(n)) and space complexity of O(n).

Having this in consideration, we can say that our final time complexity is O(n * log(n)) and our space complexity is O(n).

There is also an iterative implementation, which you can check out here

The final time and space complexity of this iterative approach are the same as in the recursive implementation.

😁 I hope this has helped!

There are other array searching algorithms that are popular, like jump search and exponential search, but I'll cover them in another post!

That's everything for now! Thank you so much for reading. If you have any questions please feel free to drop them off. Follow me if you want to read more about this kind of topics!